QAOA M$\kappa$CS#

The Max-$\kappa$-Colorable Subgraph problem and its QAOA implementation is discussed in plenty of detail in the QAOA tutorial. All the necessary ingredients and required steps to run QAOA are elaborated on in an easy to grasp manner.

Here, we provide a condensed implementation of QAOA for M$\kappa$CS using all of the predefined functions.

Problem description#

Given a Graph $G = (V,E)$ and $\kappa$ colors, maximize the size (number of edges) of a properly colored subgraph.

Cost operator#

create_coloring_operator(G)[source]#

Generates the cost operator for an instance of the coloring problem for a given graph G.

The coloring operator and applies a phase if two neighboring nodes in the graph have the same color.

Parameters:

Gnx.Graph: The graph to color.

Returns:

cost_operatorfunction: A function receiving a QuantumVariable and a real parameter $\gamma$. This function performs the application of the cost operator.

Classical cost function#

create_coloring_cl_cost_function(G)[source]#

Creates the classical cost function for an instance of the coloring problem for a given graph G.

Parameters:

Gnx.Graph: The graph to color.

Returns:

cl_cost_functionfunction: The classical cost function for the problem instance, which takes a dictionary of measurement results as input.

Coloring problem#

graph_coloring_problem(G)[source]#

Creates a QAOA problem instance with appropriate phase separator, mixer, and classical cost function.

Parameters:

Gnx.Graph: The graph to color.

Returns:

QAOAProblemfunction: A QAOA problem instance for graph coloring for a given graph G.

Example implementation#

from qrisp import QuantumArray
from qrisp.qaoa import QAOAProblem, RX_mixer, apply_XY_mixer, QuantumColor, create_coloring_cl_cost_function, create_coloring_operator
import networkx as nx
import random
from operator import itemgetter

G = nx.Graph()
G.add_edges_from([[0,1],[0,4],[1,2],[1,3],[1,4],[2,3],[3,4]])
color_list = ["red", "blue", "orange", "green"]

qarg = QuantumArray(qtype = QuantumColor(color_list, one_hot_enc=True), shape = G.number_of_nodes())
#qarg = QuantumArray(qtype = QuantumColor(color_list, one_hot_enc=False), shape = G.number_of_nodes()) # use one_hot_enc=False for binary encoding

qaoa_coloring = QAOAProblem(cost_operator=create_coloring_operator(G),
                        mixer=apply_XY_mixer, # use RX_mixer for binary encoding
                        cl_cost_function=create_coloring_cl_cost_function(G))

init_state = [random.choice(color_list) for _ in range(len(G))]
qaoa_coloring.set_init_function(lambda x : x.encode(init_state))

result = qaoa_coloring.run(qarg, depth=3, max_iter=50)

That’s it! In the following, we print the 5 most likely solutions together with their cost values.

cl_cost =create_coloring_cl_cost_function(G)

print("5 most likely solutions")
max_five = sorted(result.items(), key=lambda item: item[1], reverse=True)[:5]
for res, prob in max_five:
    print(res, prob, cl_cost({res : 1}))

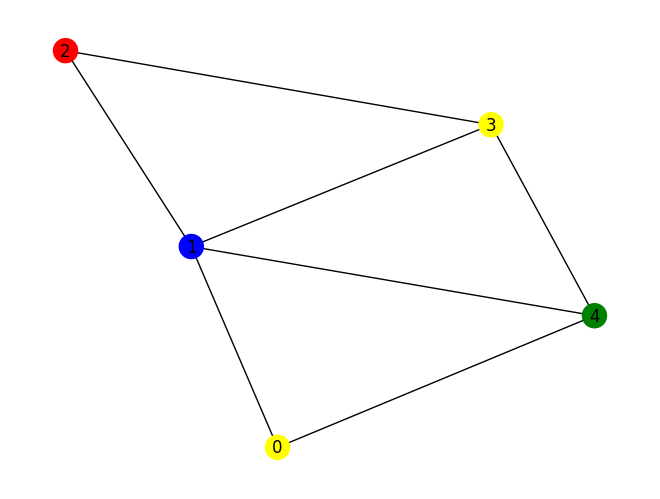
Finally, we visualize the most likely solution.

best_of_five = min([(cl_cost({item[0]:1}),item[0]) for item in max_five], key=itemgetter(0))[1]
nx.draw(G, with_labels=True, font_color='white', node_size=1000, font_size=22,
        node_color=[best_of_five[node] for node in G.nodes()],
        edge_color='#D3D3D3')